Documents Classification using Machine Learning¶
Introducing the 20newsgroups dataset¶
The 20 Newsgroups data set is a collection of approximately 20,000 newsgroup documents, partitioned (nearly) evenly across 20 different newsgroups.The 20 newsgroups collection has become a popular data set for experiments in text applications of machine learning techniques, such as text classification and text clustering.
For more information, click this link: 20newsgroups Dataset
Machine learning on the 20newsgroups dataset¶
- Framed as a supervised learning problem: Predict the label (class) of test document
- Famous dataset for machine learning of text classificaton
- Learn more about the 20newsgroups dataset: UCI Machine Learning Repository
In [1]:
# import required modules
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
import matplotlib.pyplot as plt
%matplotlib inline
Loading the 20newsgroups dataset into scikit-learn¶
In [2]:
# import 20 newsgroup dataset
from sklearn.datasets import fetch_20newsgroups
#categories = ['alt.atheism', 'comp.graphics', 'sci.space']
categories = None
data_train = fetch_20newsgroups(subset='train', remove=('headers', 'footers', 'quotes'), categories=categories)
data_test = fetch_20newsgroups(subset='test', remove=('headers', 'footers', 'quotes'), categories=categories)
In [3]:
type(data_train)
type(data_test)
Out[3]:
In [4]:
print "Train data target labels:",data_train.target
print "Test data target labels:",data_test.target
In [5]:
print "Train data target names:",data_train.target_names
print "Test data target names:",data_test.target_names
In [6]:
print "Total train data:",len(data_train.data)
print "Total test data:",len(data_test.data)
In [7]:
# Train data type
print type(data_train.data)
print type(data_train.target)
# Test data type
print type(data_test.data)
print type(data_test.target)
Requirements for working with data in scikit-learn¶
- Features and response are separate objects
- Features and response should be numeric
- Features and response should be NumPy arrays
- Features and response should have specific shapes
In [8]:
# So, first converting text data into vectors of numerical values using tf-idf to form feature vector
vectorizer = TfidfVectorizer()
data_train_vectors = vectorizer.fit_transform(data_train.data)
data_test_vectors = vectorizer.transform(data_test.data)
In [9]:
# Train data type
print type(data_train_vectors.data)
print type(data_train.target)
# Test data type
print type(data_train_vectors.data)
print type(data_train.target)
In [10]:
# check the shape of the features matrix
print data_train_vectors.shape
In [11]:
# check the shape of the response (single dimension matching the number of observations)
print data_train.target.shape
Train \ Test data¶
In [12]:
# store training feature matrix in "Xtr"
Xtr = data_train_vectors
print "Xtr:\n", Xtr
# store training response vector in "ytr"
ytr = data_train.target
print "ytr:",ytr
In [13]:
# store testing feature matrix in "Xtt"
Xtt = data_test_vectors
print "Xtt:\n", Xtt
# store testing response vector in "ytt"
ytt = data_test.target
print "ytt:",ytt
Different Classification Models¶
Multinomial Naive Bayes (MNB) classification¶
In [14]:
# import the required module from scikit learn
from sklearn.naive_bayes import MultinomialNB
In [15]:
# Implementing classification model- using MultinomialNB
# Instantiate the estimator
clf_MNB = MultinomialNB(alpha=.01)
# Fit the model with data (aka "model training")
clf_MNB.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred = clf_MNB.predict(Xtt)
print "Predicted Class Labels:",y_pred
# Predict the response score for a new observation
y_pred_score_mnb = clf_MNB.predict_proba(Xtt)
print "Predicted Score:\n",y_pred_score_mnb
K-Nearest Neighbors (KNN) classification¶
In [16]:
# import the required module from scikit learn
from sklearn.neighbors import KNeighborsClassifier
In [17]:
# Implementing classification model- using KNeighborsClassifier
# Instantiate the estimator
clf_knn = KNeighborsClassifier(n_neighbors=5)
# Fit the model with data (aka "model training")
clf_knn.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred = clf_knn.predict(Xtt)
print "Predicted Class Labels:",y_pred
# Predict the response score for a new observation
y_pred_score_knn = clf_knn.predict_proba(Xtt)
print "Predicted Score:\n",y_pred_score_knn
Support Vector Machine (SVM) classification¶
In [18]:
# import the required module from scikit learn
from sklearn.svm import LinearSVC
In [19]:
# Implementing classification model- using LinearSVC
# Instantiate the estimator
clf_svc = LinearSVC()
# Fit the model with data (aka "model training")
clf_svc.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred = clf_svc.predict(Xtt)
print "Predicted Class Labels:",y_pred
# Predict the response score for a new observation
y_pred_score_svc = clf_svc.decision_function(Xtt)
print "Predicted Score:\n",y_pred_score_svc
Evaluating & Comparing Machine Learning Models¶
Cross-Validation: K-fold¶
- Measurement of Generalization Performance
- For estimation of variation
- Divide the data into K folds
- For k = 1…K
• Train on K-1 sets leaving the kth set out for validation
• Validate on the kth set and obtain the performance metrics
- For k = 1…K
- Report the average and the variation in the performance
Diagram of 5-fold cross-validation:
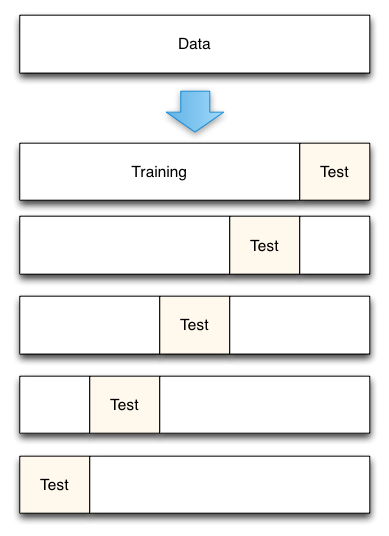
Cross-validation: Model Selection¶
In [21]:
# import the required module
from sklearn.cross_validation import cross_val_score
In [22]:
# 10-fold cross-validation with MNB model
clf_mnb = MultinomialNB(alpha=.01)
print "MultinomialNB 10-Cross Validation Score:",cross_val_score(clf_mnb, Xtr, ytr, cv=10, scoring='accuracy').mean()
In [23]:
# 10-fold cross-validation with KNN model
clf_knn = KNeighborsClassifier(n_neighbors=55)
print "KNN 10-Cross Validation Score:",cross_val_score(clf_knn, Xtr, ytr, cv=10, scoring='accuracy').mean()
In [24]:
# 10-fold cross-validation with Linear SVM model
clf_svc = LinearSVC(C=1)
print "KNN 10-Cross Validation Score:",cross_val_score(clf_svc, Xtr, ytr, cv=10, scoring='accuracy').mean()
Efficiently searching for optimal tuning parameters¶
More efficient parameter tuning using GridSearchCV¶
Allows to define a grid of parameters that will be searched using K-fold cross-validation
In [25]:
# importing the required module
from sklearn.grid_search import GridSearchCV
GridSearchCV for KNN¶
In [26]:
# define the parameter values that should be searched for KNN
k_range = range(1, 100)
weight_options = ['uniform', 'distance']
print k_range
print weight_options
In [27]:
# create a parameter grid: map the parameter names to the values that should be searched for KNN
param_grid = dict(n_neighbors=k_range, weights=weight_options)
print param_grid
In [28]:
# instantiate the grid
grid = GridSearchCV(clf_knn, param_grid, cv=10, scoring='accuracy')
In [29]:
# fit the grid with data
grid.fit(Xtr, ytr)
Out[29]:
In [30]:
# view the complete results (list of named tuples)
grid.grid_scores_
Out[30]:
In [31]:
# examine the first tuple
print grid.grid_scores_[0].parameters
print grid.grid_scores_[0].cv_validation_scores
print grid.grid_scores_[0].mean_validation_score
In [32]:
# examine the best model
print grid.best_score_
print grid.best_params_
print grid.best_estimator_
Reducing computational expense using RandomizedSearchCV for KNN¶
- Searching many different parameters at once may be computationally infeasible
RandomizedSearchCVsearches a subset of the parameters, and we control the computational "budget"
In [33]:
# importing the required module
from sklearn.grid_search import RandomizedSearchCV
In [34]:
# specify "parameter distributions" rather than a "parameter grid"
param_dist = dict(n_neighbors=k_range, weights=weight_options)
print param_dist
In [35]:
# n_iter controls the number of searches
rand = RandomizedSearchCV(clf_knn, param_dist, cv=10, scoring='accuracy', n_iter=10, random_state=5)
rand.fit(Xtr, ytr)
rand.grid_scores_
Out[35]:
In [36]:
# examine the best model
print rand.best_score_
print rand.best_params_
GridSearchCV for Multinomial Naive Bayes¶
In [48]:
# define the parameter values that should be searched for MNB
alpha = [0.001, 0.01, 0.1, 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
print alpha
In [49]:
# create a parameter grid: map the parameter names to the values that should be searched for MNB
param_grid = dict(alpha=alpha)
print param_grid
In [50]:
# instantiate the grid
grid = GridSearchCV(clf_mnb, param_grid, cv=10, scoring='accuracy')
In [51]:
# fit the grid with data
grid.fit(Xtr, ytr)
Out[51]:
In [52]:
# view the complete results (list of named tuples)
grid.grid_scores_
Out[52]:
In [53]:
# examine the first tuple
print grid.grid_scores_[0].parameters
print grid.grid_scores_[0].cv_validation_scores
print grid.grid_scores_[0].mean_validation_score
In [54]:
# examine the best model
print grid.best_score_
print grid.best_params_
print grid.best_estimator_
GridSearchCV for Linear SVM¶
In [92]:
# define the parameter values that should be searched for Linear SVM
C = range(1,100,10)
tol = [1e-2, 1e-4, 1e-9]
print "C:", C
print "Tolerance for stopping criteria:", tol
In [93]:
# create a parameter grid: map the parameter names to the values that should be searched for SVM
param_grid = dict(C=C, tol=tol)
print param_grid
In [94]:
# instantiate the grid
grid = GridSearchCV(clf_svc, param_grid, cv=10, scoring='accuracy')
In [96]:
# fit the grid with data
grid.fit(Xtr, ytr)
Out[96]:
In [97]:
# view the complete results (list of named tuples)
grid.grid_scores_
Out[97]:
In [98]:
# examine the first tuple
print grid.grid_scores_[0].parameters
print grid.grid_scores_[0].cv_validation_scores
print grid.grid_scores_[0].mean_validation_score
In [99]:
# examine the best model
print grid.best_score_
print grid.best_params_
print grid.best_estimator_
Reducing computational expense using RandomizedSearchCV for SVM¶
In [100]:
# specify "parameter distributions" rather than a "parameter grid"
param_dist = dict(C=C, tol=tol)
print param_dist
In [60]:
# n_iter controls the number of searches
rand = RandomizedSearchCV(clf_svc, param_dist, cv=10, scoring='accuracy', n_iter=10, random_state=5)
rand.fit(Xtr, ytr)
rand.grid_scores_
Out[60]:
In [61]:
# examine the best model
print rand.best_score_
print rand.best_params_
Classification Accuracy¶
- percentage of correct predictions
In [25]:
# importing the required module
from sklearn import metrics
Classification Accuracy of MultinomialNB¶
In [26]:
# Instantiate the estimator
clf_MNB = MultinomialNB(alpha=.01)
# Fit the model with data (aka "model training")
clf_MNB.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred_mnb = clf_MNB.predict(Xtt)
print "Predicted Class Labels:",y_pred_mnb
# calculate accuracy
print "Classification Accuracy:",metrics.accuracy_score(ytt, y_pred_mnb)
Classification Accuracy of KNN¶
In [27]:
# Instantiate the estimator
clf_knn = KNeighborsClassifier(n_neighbors=1, weight='distance')
# Fit the model with data (aka "model training")
clf_knn.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred_knn = clf_knn.predict(Xtt)
print "Predicted Class Labels:",y_pred_knn
# calculate accuracy
print "Classification Accuracy:",metrics.accuracy_score(ytt, y_pred_knn)
Classification Accuracy of Linear SVM¶
In [28]:
# Instantiate the estimator
clf_svc = LinearSVC(C=1, tol=0.01)
# Fit the model with data (aka "model training")
clf_svc.fit(Xtr, ytr)
# Predict the response for a new observation
y_pred_svc = clf_svc.predict(Xtt)
print "Predicted Class Labels:",y_pred_svc
# calculate accuracy
print "Classification Accuracy:",metrics.accuracy_score(ytt, y_pred_svc)
Confusion matrix¶
- Table that describes the performance of a classification model
Confusion matrix of MultinomialNB¶
In [29]:
# first argument is true values, second argument is predicted values
print metrics.confusion_matrix(ytt, y_pred_mnb)
Confusion matrix of KNN¶
In [30]:
# first argument is true values, second argument is predicted values
print metrics.confusion_matrix(ytt, y_pred_knn)
Confusion matrix of Linear SVM¶
In [31]:
# first argument is true values, second argument is predicted values
print metrics.confusion_matrix(ytt, y_pred_svc)
Metrics computed from a confusion matrix¶
Classification Error: Overall, how often is the classifier incorrect?
- Also known as "Misclassification Rate"
In [32]:
print "Classification Error of MultinomialNB:", 1 - metrics.accuracy_score(ytt, y_pred_mnb)
print "Classification Error of KNN:", 1 - metrics.accuracy_score(ytt, y_pred_knn)
print "Classification Error of LinearSVC:", 1 - metrics.accuracy_score(ytt, y_pred_svc)
Sensitivity: When the actual value is positive, how often is the prediction correct?
- How "sensitive" is the classifier to detecting positive instances?
- Also known as "True Positive Rate" or "Recall"
In [33]:
print "Sensitivity of MultinomialNB:",metrics.recall_score(ytt, y_pred_mnb, average='weighted')
print "Sensitivity of KNN:",metrics.recall_score(ytt, y_pred_knn, average='weighted')
print "Sensitivity of LinearSVC:",metrics.recall_score(ytt, y_pred_svc, average='weighted')
Precision: When a positive value is predicted, how often is the prediction correct?
- How "precise" is the classifier when predicting positive instances?
- TP / (TP + FP)
In [34]:
print "Precision of MultinomialNB:", metrics.precision_score(ytt, y_pred_mnb, average='weighted')
print "Precision of KNN:", metrics.precision_score(ytt, y_pred_knn, average='weighted')
print "Precision of LinearSVC:", metrics.precision_score(ytt, y_pred_svc, average='weighted')
F-measure:
- 2 P R / (P + R)
In [35]:
print "F-measure of MultinomialNB:", metrics.f1_score(ytt, y_pred_mnb, average='weighted')
print "F-measure of KNN:", metrics.f1_score(ytt, y_pred_knn, average='weighted')
print "F-measure of LinearSVC:", metrics.f1_score(ytt, y_pred_svc, average='weighted')
Specificity: When the actual value is negative, how often is the prediction correct?
- How "specific" (or "selective") is the classifier in predicting positive instances?
- TN / (TN + FP)
False Positive Rate: When the actual value is negative, how often is the prediction incorrect?
- FP / (TN + FP)
True Positive Rate: When the actual value is positive, how often is the prediction correct?
- TP / (TP + FP)
ROC Curves and Area Under the Curve (AUC)¶
In [36]:
# importing the required modules
from sklearn.metrics import roc_curve, auc
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
In [70]:
def ROC_multi_class(Xtr, ytr, Xtt, ytt, clf):
classes = [0,1, 2, 3, 4]
# Binarize the output
ytr = label_binarize(ytr, classes=classes)
n_classes = ytr.shape[1]
# Learn to predict each class against the other
classifier = OneVsRestClassifier(clf)
classifier.fit(Xtr, ytr)
if (clf == clf_svc):
y_pred_score = classifier.decision_function(Xtt)
else:
y_pred_score = classifier.predict_proba(Xtt)
ytt = label_binarize(ytt, classes=classes)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(ytt[:, i], y_pred_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Plot ROC curves for the multiclass
for i in range(n_classes):
plt.plot(fpr[i], tpr[i], label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i+1, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC of multi-class')
plt.legend(loc="lower right")
plt.show()
Multi-class ROC of Multinomial Naive Bayes¶
In [71]:
# ROC for MultinomialNB
print "ROC and AUC of MultinomialNB"
ROC_multi_class(Xtr, ytr, Xtt, ytt, clf_MNB)
In [72]:
# ROC for KNeighborsClassifier
print "ROC and AUC of KNN"
ROC_multi_class(Xtr, ytr, Xtt, ytt, clf_knn)
In [73]:
# ROC for LinearSVC
print "ROC and AUC of LinearSVC"
ROC_multi_class(Xtr, ytr, Xtt, ytt, clf_svc)
PR Curves and Area Under the Curve PR (AUC-PR)¶
In [41]:
# importing the required module
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
In [74]:
def PR_multi_class(Xtr, ytr, Xtt, ytt, clf):
classes = [0,1, 2, 3, 4]
# Binarize the output
ytr = label_binarize(ytr, classes=classes)
n_classes = ytr.shape[1]
# Learn to predict each class against the other
classifier = OneVsRestClassifier(clf)
classifier.fit(Xtr, ytr)
if (clf == clf_svc):
y_pred_score = classifier.decision_function(Xtt)
else:
y_pred_score = classifier.predict_proba(Xtt)
ytt = label_binarize(ytt, classes=classes)
# Compute Precision-Recall and plot curve
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(ytt[:, i], y_pred_score[:, i])
average_precision[i] = average_precision_score(ytt[:, i], y_pred_score[:, i])
for i in range(n_classes):
plt.plot(recall[i], precision[i], label='PR curve of class {0} (area = {1:0.2f})'
''.format(i+1, average_precision[i]))
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve of multi-class')
plt.legend(loc="lower right")
plt.show()
In [75]:
# PR curve of MultinomialNB
print "PR and AUC of MultinomialNB"
PR_multi_class(Xtr, ytr, Xtt, ytt, clf_MNB)
In [76]:
# PR curve of KNeighborsClassifier
print "PR and AUC of KNN"
PR_multi_class(Xtr, ytr, Xtt, ytt, clf_knn)
In [77]:
# PR curve of LinearSVC
print "PR and AUC of LinearSVC"
PR_multi_class(Xtr, ytr, Xtt, ytt, clf_svc)
Benchmarking of Different Classifiers¶
Diagram of Benchmarking of different Classifiers:
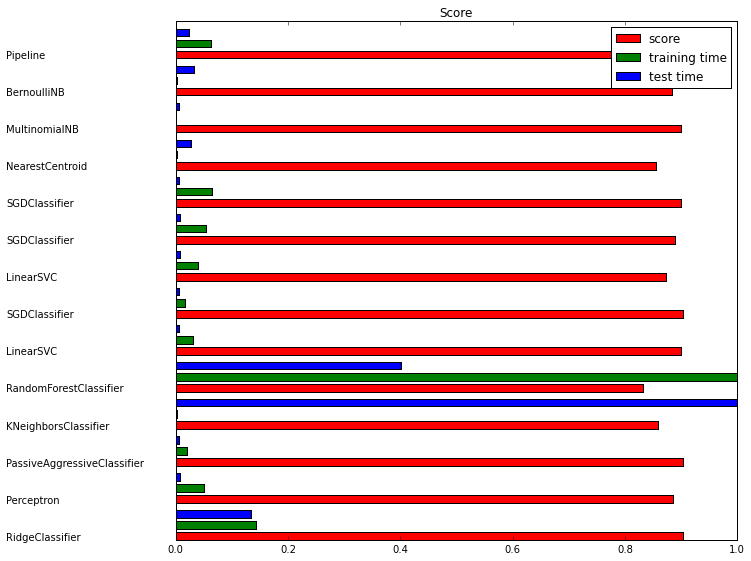
References¶
- https://en.wikipedia.org/wiki/Machine_learning
- http://scikit-learn.org/stable/modules/svm.html
- http://scikit-learn.org/stable/tutorial/basic/tutorial.html
- http://scikitlearn.org/stable/modules/grid_search.html
- http://scikit-learn.org/stable/datasets/twenty_newsgroups.html
- http://scikit-learn.org/stable/auto_examples/text/document_classification_20newsgroups.html#example-text-document-classification-20newsgroups-py
- http://scikit-learn.org/stable/auto_examples/model_selection/grid_search_text_feature_extraction.html#example-model-selection-grid-search-text-feature-extraction-py
- https://en.wikipedia.org/wiki/Sensitivity_and_specificity
- https://en.wikipedia.org/wiki/Sensitivity_and_specificity
- http://scikitlearn.org/stable/modules/generated/sklearn.metrics.roc_curve.html
- http://scikitlearn.org/stable/auto_examples/model_selection/plot_roc.html#example-model-selection-plotroc-py
- http://scikitlearn.org/stable/model_selection.html